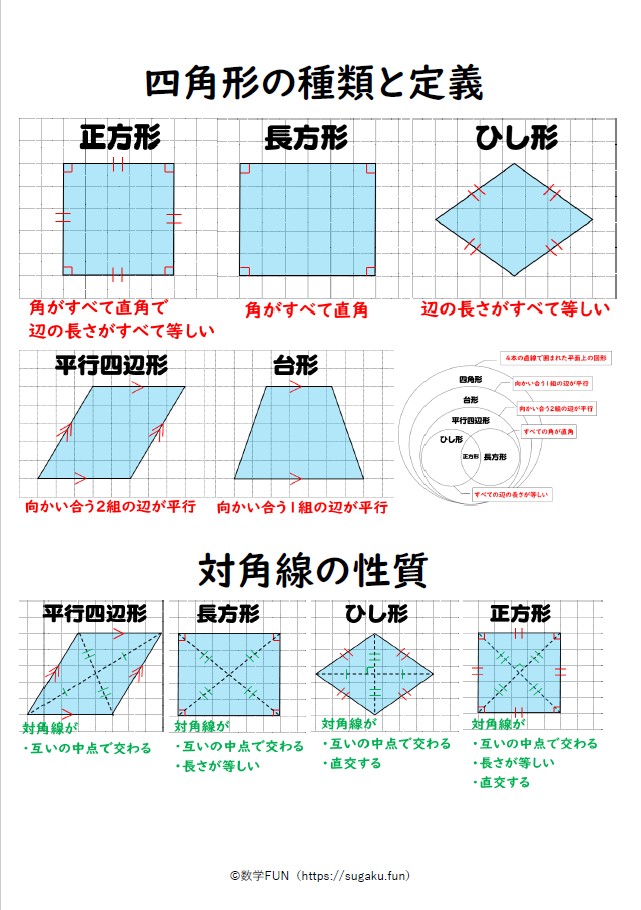
4つの辺が全て等しい四角形 正方形の定義 4つの角が全て等しく、4つの辺が全て等しい四角形 対角線の定義 長方形の対角線は長さが等しい ひし形の対角線は垂直に交わる 特別な平行四辺形になるための条件 一つの内角が直角⇒長方形 対角線が等しい四角形 4本の直線で囲まれた図形 角が4つある。 角の総和は360°である。 対角線が2本ある。 長方形 すべての角が直角の四角形 向かい合う辺が平行である。 向かい合う辺の長さが等しい。 対角線の長さが等しい。 線対称、点対称な図形である。つまり,「対角線→四角形」の順です。 はじめは同じ長さの棒を使って四角形を作りま す。正方形・長方形・台形はできますが,平行四辺 形やひし形はできません。「ちがう長さの棒がほし い」という子どもたちの声に答えて別の棒をわたす

高校数学 円に内接する四角形の対角線の長さと面積 受験の月
対角線の長さが等しい四角形は
対角線の長さが等しい四角形は- ● 円に内接する四角形の内角は、その対角の外角と等しい まず、円に内接する四角形では ∠ A ∠ C = 180 ° が成り立ちます。 対角の和が 180 ° になる理由は、 円周角の定理 から説明できます。 円の中心を点 O 、 ∠ A = θ とおくと 🔄 最終更新日 19年12月11日 by takara_semi 中2 > 5章:三角形と四角形 本章では三角形と四角形の性質を調べます。特に線対称な図形である二等辺三角形や、点対称な図形である平行四辺形の性質を詳しく調査し、その性質を証明してみましょう。




教えてください 至急です Clear
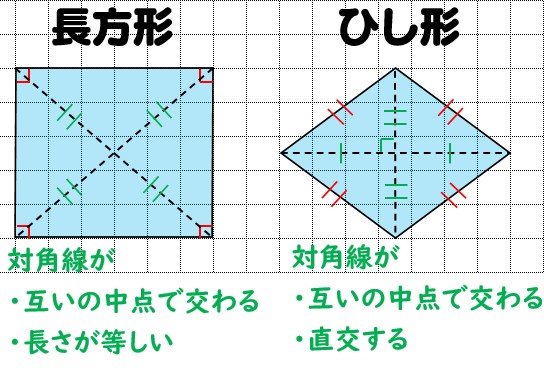
例題1:図のような四角形の面積を求めよ。 対角線が直角に交わる場合には、対角線の長さをかけ算して 2 で割れば面積を求めることができます。 この場合、面積は 4 × 5 ÷ 2 = 10 c m 2 となります。 では、この公式が成り立つ理由を説明します。 (対角線平行四辺形: 対角線が 互いの中点で交わる 長方形: 対角線が 互いの中点で交わる & 長さが等しい ひし形: 対角線が 互いの中点で交わる & 直交する 正方形: 対角線が 互いの中点で交わる & 直交する & 長さが等しい対角線 〈条件〉 〈答え〉 ア2本の対角線の長さが等しい。 1 イ2本の対角線が垂 すい 直 ちょく に交わる。(2本の対角線が 2 交わってできる角が直角(90°)。) 3 ウ2本の対角線が交わる点から向かい
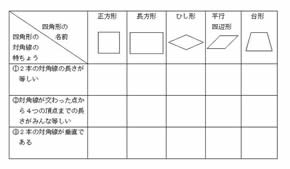
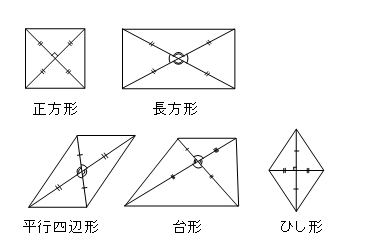
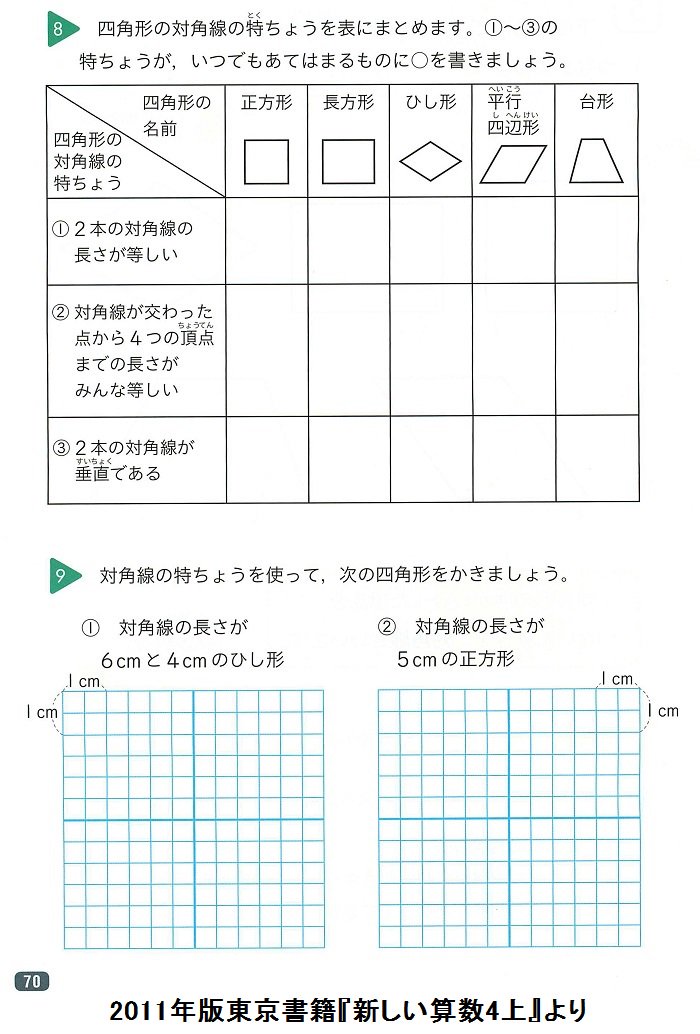
(2)対角線 基本 の確かめ 下の5つの 四角形 に,それぞれ 2本の対角線 をひいて ,対角線 の長さや 交わり 方について , ①~③にあてはまるものを 選んで 丸を書きましょう 。 長方形正方形台形 平行四辺形 ひし 形 ①2 本の対角線 の長さが 等しい 。 対角線の長さが等しい平行四辺形は長方形である事を平行四辺形ABCDでAC=BDであるとして証明 ベストアンサー:四角形ABCDの対角線AC、BDの交点をOとする AC=BD、かつ、平行四辺形の対角線は中点で交わるので AO=BO=CO=DO① △ABOは①より2等 3対角線が垂直に交わる四角形があります。2本の対角線の長さが次のとき、四角形の面積を求めなさい。 (1)16cm、14cm (2)18cm、11cm (3)13cm、7cm 式と解説を願います。
1組の等しい対辺の長さをa、他の辺をb、cとし、1組の等しい対角の大きさをθとしますと、余弦定理から、対角線について次の関係が得られます。 a^2b^22ab cosθ=a^2c^22ac cosθ ⇔ (bc) (bc2a cosθ)=0 ∴b=c または bc=2a cosθ ここで、b=cですと平行四辺形に 間違ってたらごめんなさい(^ ^;) ① 対角線の長さが等しい四角形 角から真反対の角の線を引く(全ての四角形に)⇦四角形の図はないのであれば教科書等の四角形を参考にする) その四角形の二つの対角線の長さが等しい四角形が答えである。 ②二つの対角線が混じった時にできる角度 例)+⇦ウ 向かい合う角は等しい。 エ 対角線はそれぞれの中点で交わる。 オ 対角線の長さは等しい。 6 「平行四辺形の対角線はそれぞれの中点で交わる」こと を,次のように証明しました。 上の証明の に当てはまる合同条件を,下のア



四角形 12時目




正方形 Wikipedia
反例 対角線の長さが等しい台形を描くことができる。 対角線の長さが等しい四角形は、必ずしも 長方形 ではない。 「 ひし形は、対角線が垂直に交わる四角形 である。」 という言葉は、正しい。 しかし、 平行四辺形の対角線は(それぞれの中点 )で交わる。 4 次の問いに答えなさい。 (1)ひし形,長方形,正方形について,それぞれの定義と対角線についての性質を書け。 ひし形 (定義) 4つの辺が等しい四角形 (性質) 対角線は垂直に交わる。対角線などの長さ/錐や柱の体積など/立体上2組の対辺がそれぞれ平行な四角形を平行四辺形と言う。 平行四辺形には、 ・向かい合う辺の長さが等しい ・向かい合う角の大きさが等しい ・対角線が互いに中点で交わる という3つの重要な性質が



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf



立体切断の切り口 これひし形なの 長方形かと思った の解き方について 算田数太郎の中学受験ブログ
長方形,正方形,台形,平行四辺形,ひし形の対角線の長さや交わり方について,次のア, イ,ウにあてはまるものを選び, を書きましょう。 長方形 正方形 台形 平行四辺形 ひし形 ア 2本の対角線の長さが等しい。対角線は、互いの長さを2 等分する。 凹四角形 内角の大きさが180°(π ラジアン) を超えるような頂点を持つ四角形。対角線が四角形の内部で交点を持たない、外角が定義できないなどの不都合があるため、日本の初等中等教育では「矢じり形」などと 凹四角形 内角の大きさが180°(π ラジアン) を超えるような頂点を持つ四角形。対角線が四角形の内部で交点を持たない、外角が定義できないなどの不都合があるため、日本の初等中等教育では「矢じり形」などと呼んで、四角形の集合には含めない。



台形 平行四辺形 ひし形 対角線とは 1



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学
な四角形 二組の対辺が それぞれ平行な 四角形 四辺の長さが 等しい四角形 4つの角が 90度の四角形 四辺の長さが等し く、かつ 4つの角が90度 の四角形 角度 二組の対角がそれ ぞれ等しい 二組の対角がそれ ぞれ等しい 辺 二組の対辺の長さ がそれぞれ等しい凧形 ( kite ):それぞれ長さの等しい2辺によってはさまれた対角を持つ四角形。 対角線の1つが線対称の軸となり、残り一組の対角は等しい大きさを持つ。 2本の対角線は、互いに直交する。平行四辺形の定理(2組の対角がそれぞれ等しい)より、 ∠A=∠C A D∠B=∠D ∠A+∠B=180° (同側内角の和)∠A=90°にすると ∠C=90°∠B=∠D=90°
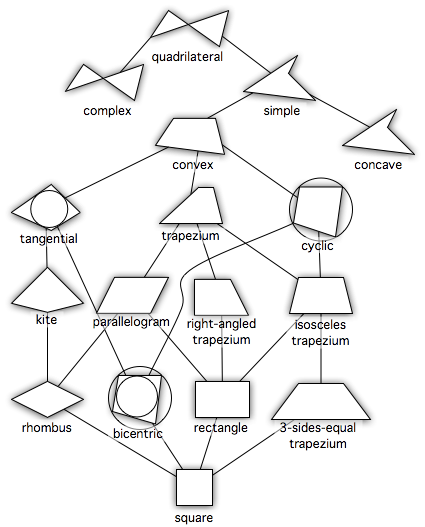



四角形 Wikipedia



2
3年選択授業 四角面和の実践記録 下図を示す。 (長方形、対角線) T この図の中にどんな図形がありますか? T この図を見て、どんなことに気づきますか? S 合同な図形がある。 錯角、対頂角がある。 対角線の長さは等しい。 4つの三角形の面積は 対角線の長さとなす角で表された四角形の面積公式 S=1/2pqsinθ(裏技)の証明、対角線の長さの和が一定である四角形の面積の最大 スポンサーリンク 高校数学Ⅰ 三角比と図形の計量① 長方形の2本の対角線の長さは等しい ② ひし形の対角線は垂直に交わる ③ 台形は2つの平行な辺でできている ④ 平行四辺形のすべての辺の長さは等しい ――――――――




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



2
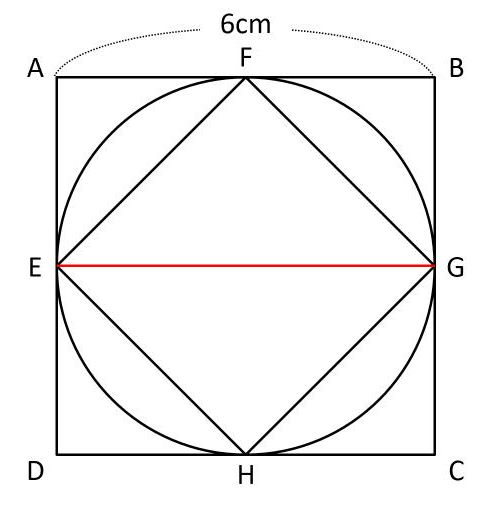
正方形の対角線の長さを求める方法 具体例で学ぶ数学 > 図形 > 正方形の対角線の長さを求める方法 最終更新日 (正方形の対角線の長さ) = (1辺の長さ) × 2 おおよそ、 1414 × (1辺の長さ) 目次 具体例 例題 解答 2.対角線の長さを等しくする。 のどちらかをすると長方形になります。 長方形もひし形も平行四辺形の特殊な形ですからね 長方形の対角線は等しいというか 対角線を等しくすると長方形になる って方が正しいんですけどね「面積= (対角線 1 × 対角線 2)/2」すなわち「A = (d 1 × d 2)/2」 例: 対角線の長さが19mと5mのたこ形があるとします。これの面積は、(19 × 5)/2 = 95/2 = 475 ㎡です。 対角線の長さが分からず、測ることもできない場合、三角関数を用いて求めることができます。




ボード 勉強 のピン




これの答えは 対角線が垂直に交わる となり合う辺が等しい Clear
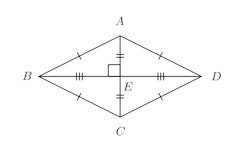
正方形 ⇒ 全ての辺の長さ・角度が等しい四角形 ひし形と対角線の関係 ひし形の対角線は直角に交わります。下図をみてください。ひし形に対角線を2本引きました。 このとき対角線は中点(真ん中の点)で交わります。平行四辺形の続き 次に,長方形,ひし形,正方形の性質を扱いましょう. 定義 1.4つの角が等しい四角形を長方形という. 2.4辺の長さが等しい四角形をひし形という. 3.4つの角が等しくかつ4辺の長さの等しい四角形を正方形という. まず,長方形(2組の対角の大きさがそれぞれ等しい四角形の、向 かい合う頂点同士をむすんだ直線のことを、対 角線といいます。 ・2 本の対角線が、それぞれのまん中の点で交わる四角形平 行四辺形、ひ し形、長 方形、正方形 ・2 本の対角線の長さが等しい四角形長 方形、正方形



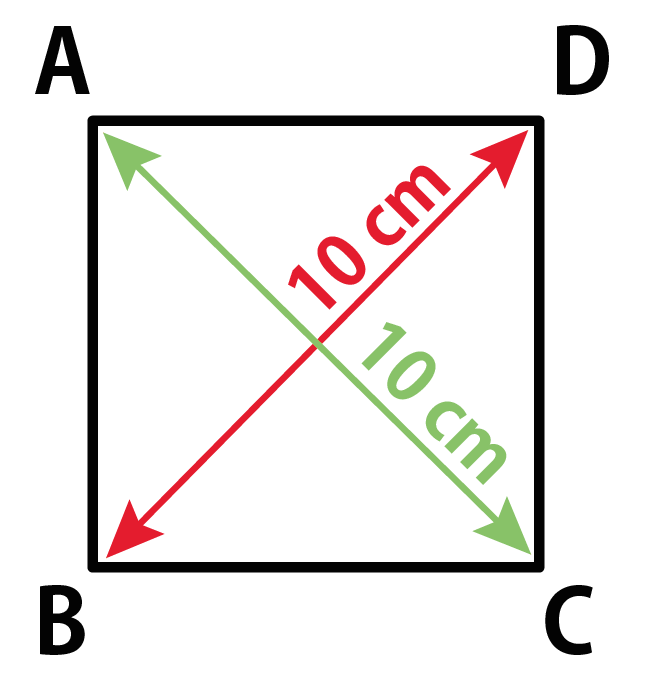
数学の質問です 対角線の長さが等しい四角形は 長方形である Yahoo 知恵袋




対角線の学習 ますます算数
まとめ:長方形の対角線の長さはやっぱり等しい。 長方形の性質の、 対角線の長さはそれぞれ等しい はおさえておこう! 三角形の合同で簡単に証明できるから安心だね。 そん 台形 対角線 対角線が直交しない場合はどうすればよいでしょうか 実は対角線が直角に交わらない場合でも対角線の長さと面積の間には関係がありますただし高校数学で習う三角比の考え方が必要です どんな四角形でも対角線のなす角を theta とおくと12)「対角線の長さが等しい四角形は、長方形か正方形に必ずなりますか。」 13)同じ長さの対角線で四角形を描かせてみる。(ならない四角形もある。) 14)対角線を交点で2等分させて、四角形を作らせる。 15)p118の(1)の作図問題をさせる。



1宿題で2本の対角線の長さが等しい四角形24つの辺の長さが全て等しい Yahoo 知恵袋
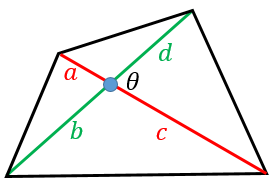



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学



Happylilac Net 4nen Sikakukei Ans 05 Pdf



1宿題で2本の対角線の長さが等しい四角形24つの辺の長さが全て等しい Yahoo 知恵袋




解説お願いします 性質的なものが理解できなくて 223 Clear
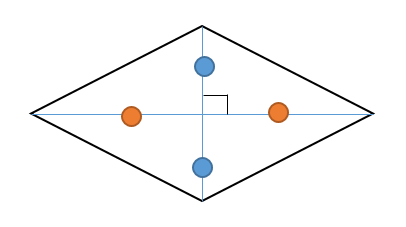



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー



2



Http Www Tome Svr Jp Tsuyama Chu Html Action Common Download Main Upload Id 29



2



2
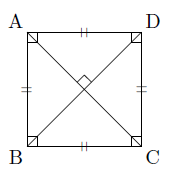



正方形 まなびの学園




なんでこうなるのか教えてください Clear



台形 平行四辺形 ひし形 対角線とは 1



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係



2




四角形 Wikipedia



中2数学 平行四辺形の証明のポイントと練習問題 Examee
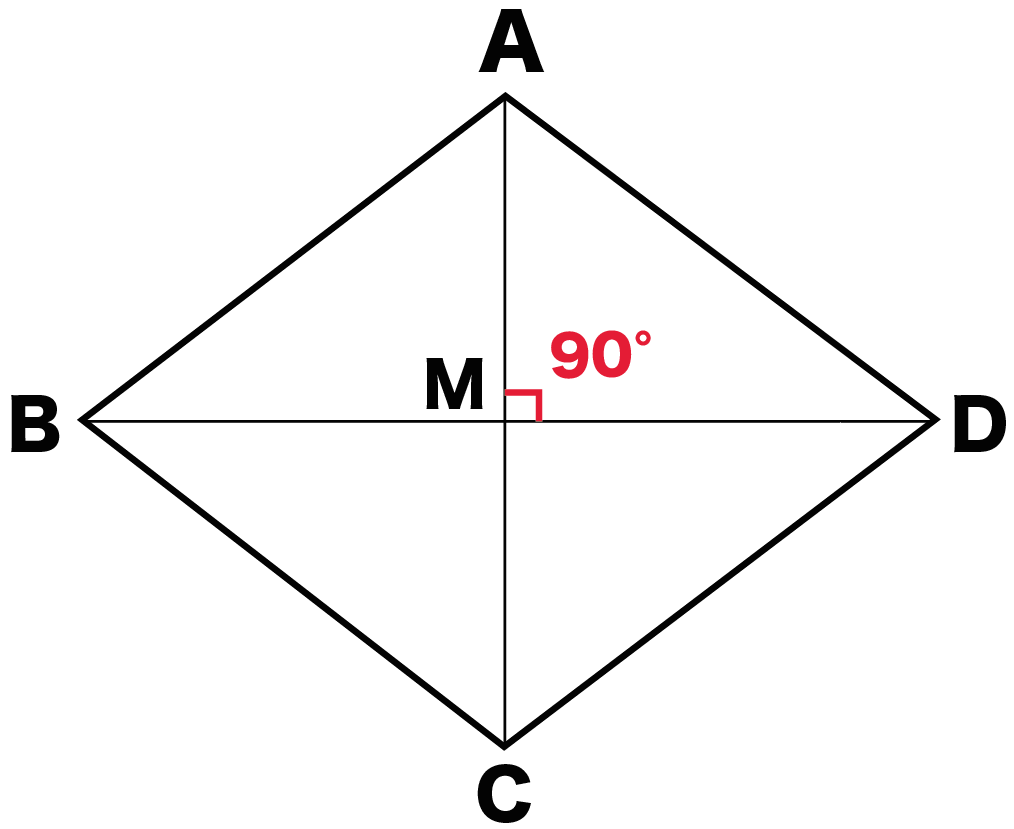



ひし形の性質 対角線はなぜ垂直に交わるのか Qikeru 学びを楽しくわかりやすく



数学の質問です 対角線の長さが等しい四角形は 長方形である Yahoo 知恵袋




算数 小4 19 四角形の特ちょう Youtube



2



1




教えてください 至急です Clear



2組の対辺がそれぞれ等しい四角形は何ですか 又 対角線の長さが等 Yahoo 知恵袋



2




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



2




高校数学 円に内接する四角形の対角線の長さと面積 受験の月




等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学



対角線で参観 教育考現学



ひし形 菱形 とは 定義や面積の求め方 公式 計算問題 受験辞典
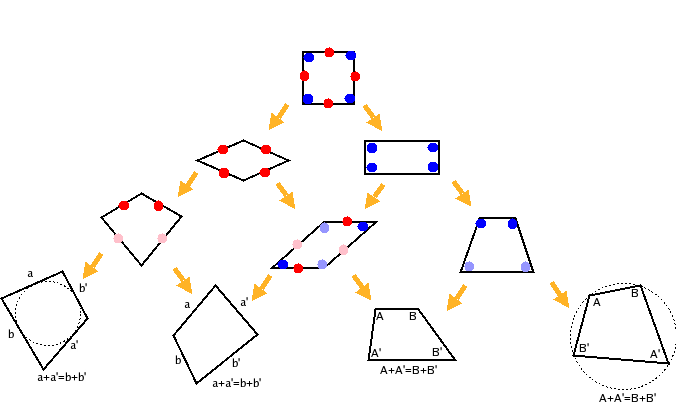



四角形の分類 低次元日記
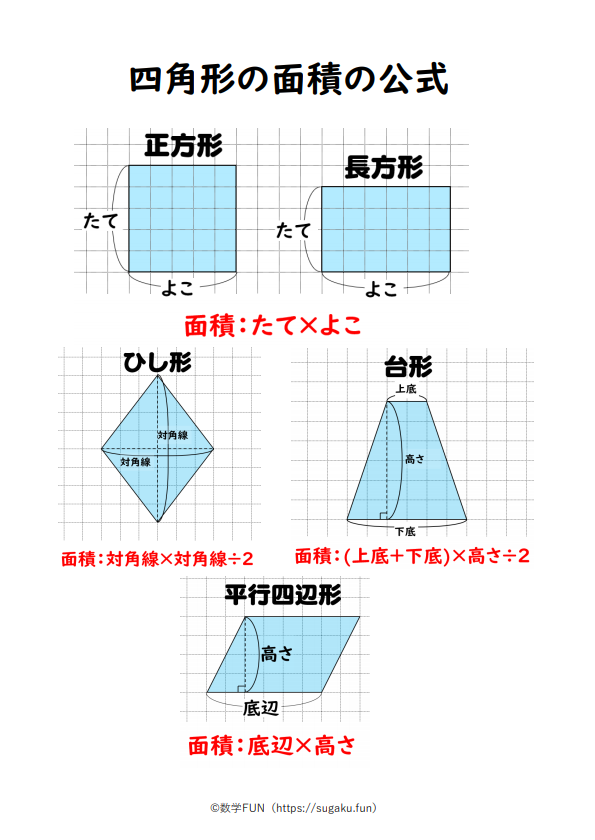



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
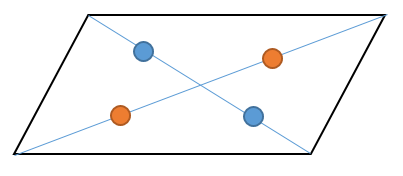



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー
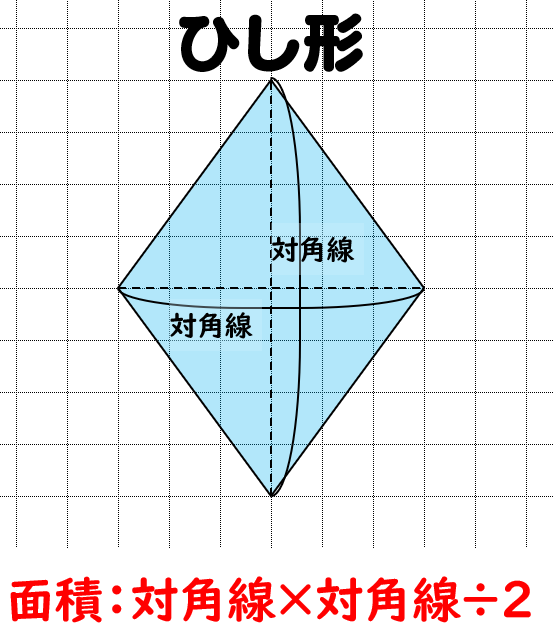



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



Www Pref Kanagawa Jp Documents 4 C Pdf




算数1日1題 15 11 15 対角線 解説編 Youtube



簡単公式 対角線で正方形の面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく




無料の学習プリント 小学4年生の算数ドリル いろいろな四角形 みそにゃch



四角形の対角線 レッツスタディー



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ




ひし形 の 条件




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月




ひし形の面積の求め方 公式と計算例



図形の扉 四角形の性質




中学数学 特別な平行四辺形について Clear




対角線と四角形 Youtube




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



2本の対角線の長さが等しい四角形は長方形ですか 長方形とは限りません 例 Yahoo 知恵袋



ひし形の面積は 1分でわかる求め方 公式 辺の長さ 対角線との関係




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



Dqmqbittylolmm



Http Kylaboratory Com Wp Wp Content Uploads 18 10 17f60aa7f52cdd6a27f9d7ef858 1 Pdf



1




小学4年生の算数 動画 四角形の特ちょうの問題 19ch



証明



いろいろな四角形 四角形の対角線 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材
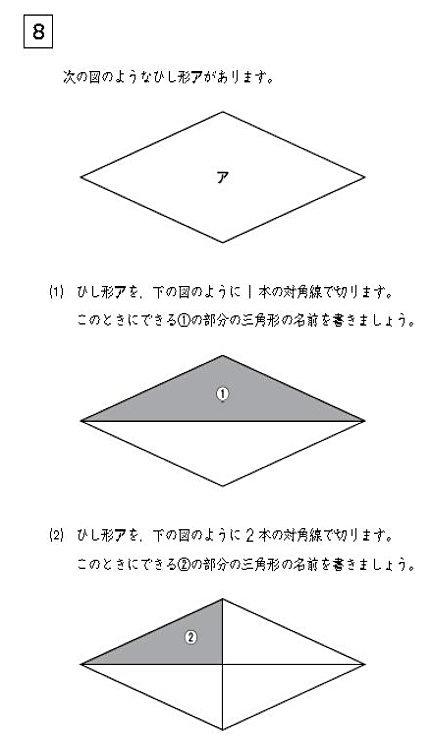



実践記録算数5年



平面図形の基礎




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



Www Joes Or Jp Cms Joes Pdf Kojin Tsushin Sansu Note Pdf



ねこ騙し数学



3



1



黒木玄 Gen Kuroki 掛算 参考資料3 4 問題緑三角8に注目 この問題の出し方を見ると 東京書籍は 正方形は長方形でもひし形でも平行四辺形でも台形でもない などなどの立場で子供に算数を教えるという方針のように見える T Co 0iis4v5ak3




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




対角線 数学の記録



Http Www Pref Osaka Lg Jp Attach 6629 Jmw 2b5 9 Pdf
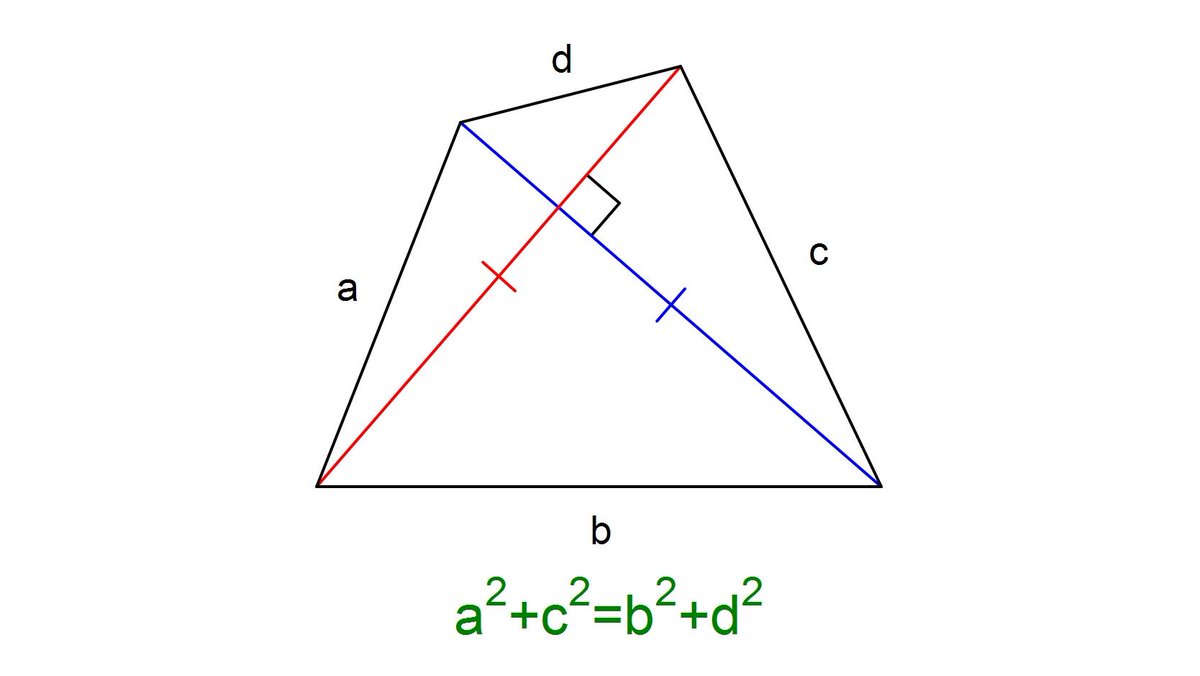



ポテト一郎 Sur Twitter 対角線の長さが等しく垂直に交わる四角形 辺の長さに次の関係があります



正方形 Wikipedia




3 Abcd Ab Da Descubre Como Resolverlo En Qanda
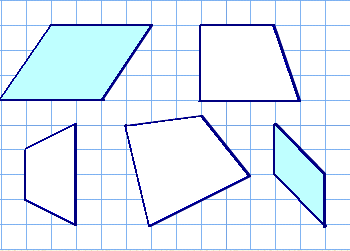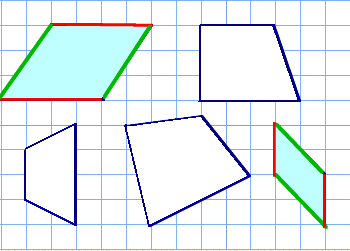



4年算数 垂直 平行と四角形 2 教え方




正方形の数 公式 正方形の面積を求める公式は 正方形の面積 一辺 一
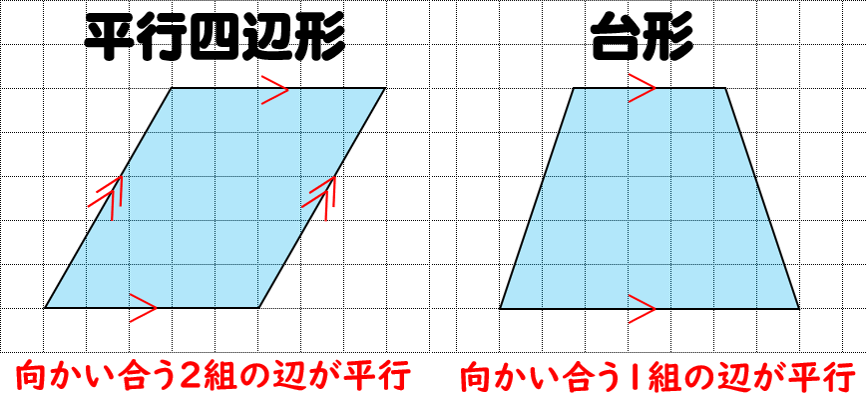



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




長方形の性質 対角線の長さはなぜ等しいのか Qikeru 学びを楽しくわかりやすく




正方形と長方形のせいしつ 小学生4年生 小学生の算数が基礎から子どもは学べ 大人は教えられる算数サイト



Http Sansutp Com A12 14 Pdf
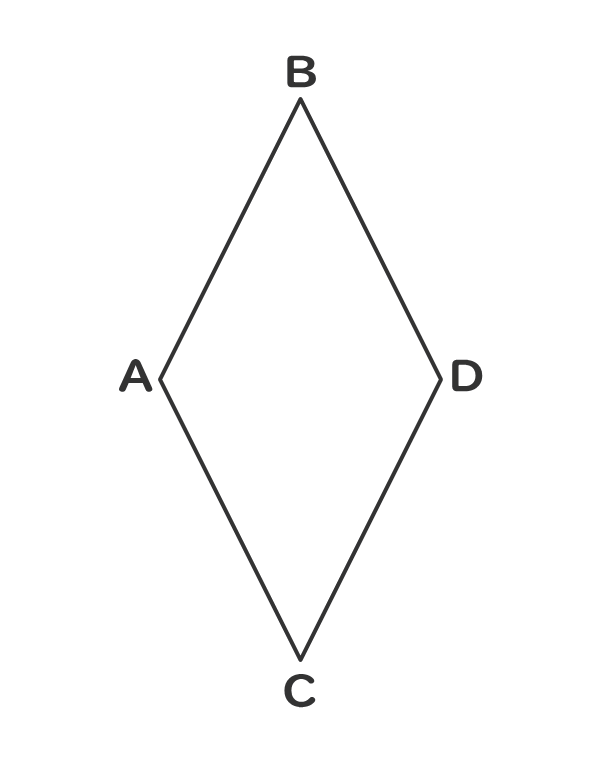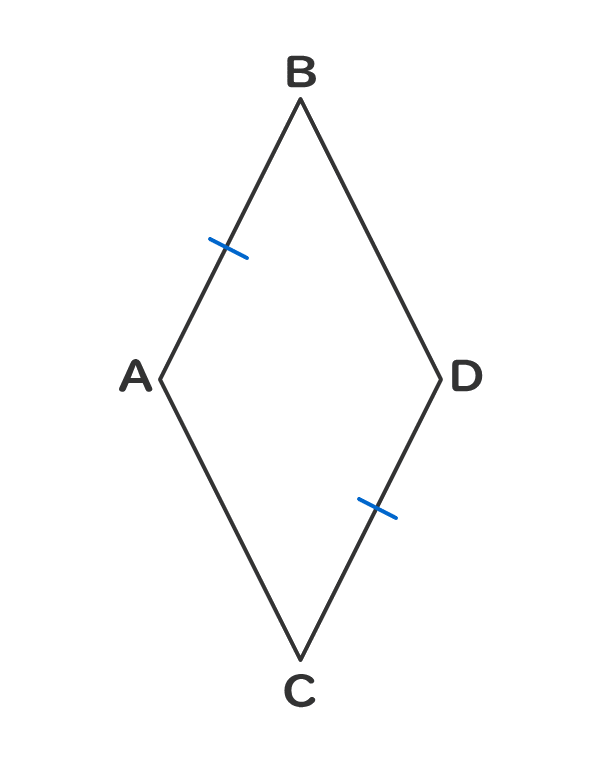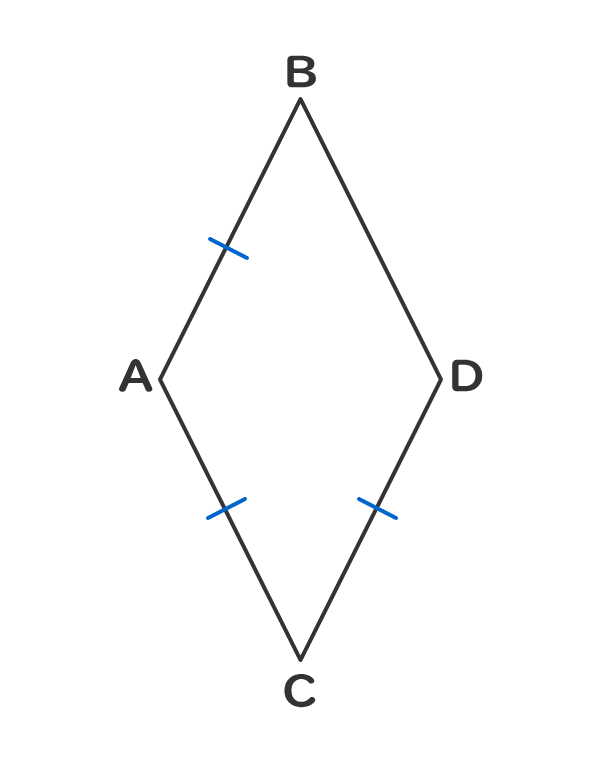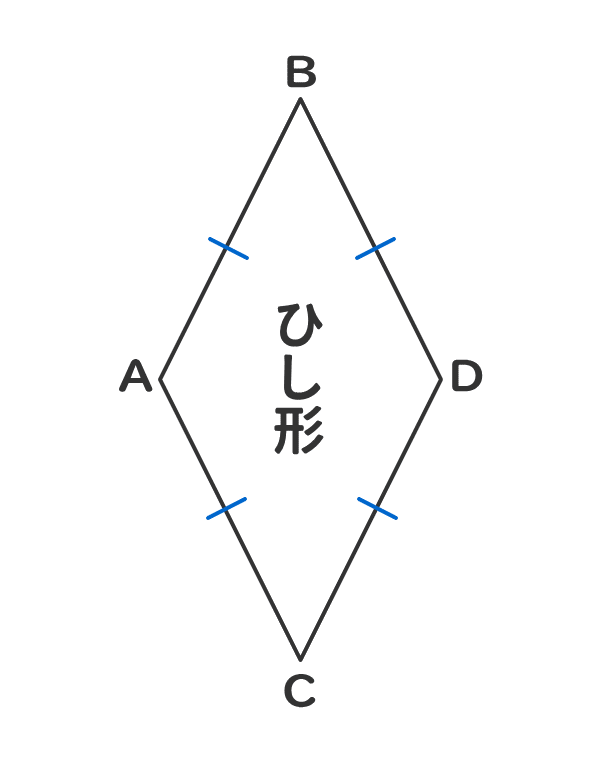



平行四辺形の仲間を知ろう 電験3種web
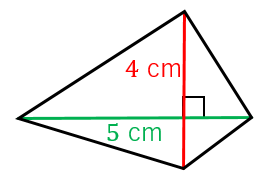



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf




中2数学 長方形の対角線 5分で学習 Youtube



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



ひし形 菱形 とは 定義や面積の求め方 公式 計算問題 受験辞典



すごく恥ずかしい質問なのですが 対角線の長さを変えなかった Yahoo 知恵袋



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



1 長方形ならば対角線は等しいが 対角線が等しい平行四辺形は Yahoo 知恵袋



0 件のコメント:
コメントを投稿